1 is not exactly 1
오늘 다뤄볼 내용은, 컴퓨터 연산에 있어서 컴퓨터가 명확하게 나타내지 못하는 수들에 대해 다뤄보려고 한다. 다소 길지만 끝까지 읽으면 분명 도움이 될 것이다.
개발자 기술 면접에서도 단골로 차용되는 주제이다.
- 실제로 나도 기술 면접에서 이 주제로 면접을 봤었고 굉장히 좋은 평을 들었다.
- 어디가서 부동 소수점 계산 면접을 보게된다면 이 자료면 충분할 것이다.
Java Code
@Test
void test() {
System.out.println(0.1 * 10);
System.out.println(0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1);
}
위의 코드를 보면, 하나는 0.1에 10을 곱한 값을 출력하고, 하나는 0.1을 10번 더한 값을 출력한다.
직관적으로 계산해보면, 두 값은 모두 1이 된다.
하지만 결과값을 보면 다음과 같다.
1.0
0.9999999999999999
컴퓨터에서의 floating 저장
이유를 살펴보기 전에 알아야 할 것이 있다!
바로 컴퓨터가 어떻게 실수(float, double)들을 저장하는 지에 대한 것이다. 이 부분은 어떻게 보면 좀 깊은 내용을 다루는 것일 수 있다.
모두가 알다시피 컴퓨터는 0과 1만 저장할 수 있다.
즉 2진법으로 숫자를 저장한다는 것인데, 이는 정수를 저장하는데 있어서는 모든 수를 표현할 수 있지만, 소수를 저장하는데 문제가 생기게 된다.
예시
\(0.01_2 = 0.25\) 를 의미.
- 2진수 0.01은 10진수 0.25와 같다.
이런식으로 계산하다보면
\(0.1_2 = 0.5\)
\(0.01_2 = 0.25\)
\(0.001_2 = 0.125\)
\(0.0001_2 = 0.0625\)
…
와 같은 식으로 이진수가 표현이 된다.
0.3을 컴퓨터에 저장하기
그런데 문제는 \(0.3\) 을 표현하는데 생긴다.
\(0.01_2 + 0.0001_2 = 0.28125\) 이고,
따라서 \(0.3 = 0.0101...._2\) 가 될 수 있다.
하지만, \(0.3\) 은 2진수로 정확하게 나타낼 수 없다.
그 이유는 \(0.3\) 을 2로 계속 곱하여도, 값이 정리되지 않는 부분에서도 확인할 수 있다. (이 부분은 다소 수학적 부분)
2진수를 10진수로 변환할 때는,
2를 계속해서 곱하면서 일의 자리 숫자가 1이 될 경우, 2진수에서 1을 표시하고 계속해서 연산한다.
이는 곱한 결과가 0.0, 즉 나머지가 없을 때까지 계속해서 진행한다.
예시
\(0.5 * 2 = 1.0\)
\(0.5 = 0.1_2\)
- 10진수 0.5와 2진수 0.1이 같음을 확인할 수 있다.
동일하게,
\(0.25 * 2^2 = 1.0\)
\(0.25 = 0.01_2\)
그럼 \(0.1\) 을 2진수로 바꿔보도록 하자.
- \(0.1 * 2 = 0.2\) , \(0.0..._2\)
- 2를 곱해도 1의 자리 숫자가 0 이므로 0.0
- \(0.2 * 2 = 0.4\) , \(0.00..._2\)
- 2를 곱해도 1의 자리 숫자가 0 이므로 0.00
- \(0.4 * 2 = 0.8\) , \(0.000..._2\)
- 2를 곱해도 1의 자리 숫자가 0 이므로 0.000
- \(0.8 * 2 = 1.6\) , \(0.0001..._2\)
- 2를 곱하니 1의 자리 숫자가 1 이므로 \(0.0001\)
- \(0.6 * 2 = 1.2\) , \(0.00011..._2\)
- 위에서 1의 자리 숫자를 뺀 0.6을 base로 2를 곱한다
- 2를 곱하니 1의 자리 숫자가 1 이므로 \(0.00011\)
- \(0.2 * 2 = 0.4\) , \(0.000110..._2\)
이런 식으로 0.1에 맞는 2진수를 계산할 수 있다.
위 계산 식을 통해 0.1은 2진수로 완벽하게 나타낼 수 없는 무한소수(2진수에서)가 되는 것을 확인할 수 있다.
위의 수식을 통해, 0.1과 0.3을 비롯한 여러 숫자들이 2진수로 명확하게(유한소수로) 나타낼 수 없는 것을 확인할 수 있다.
IEEE standard 754
그렇다면 컴퓨터는 어떻게 0.3, 0.1이란 수를 표현할 수 있을까?
IEEE standard 754 표준을 보면 이를 알 수 있다. IEEE 754에서는 실수에 대해 이렇게 표기하도록 명시한다.
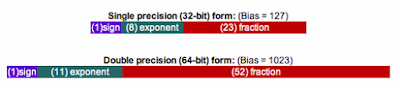
일반적으로 float 타입이 32bit, double 타입이 64bit이므로, single precision이 float 타입, double precision이 double 타입이라고 생각할 수 있다.
sign bit: 말 그대로 음수인지, 양수인지에 대한 표현.
fraction: 소수점에 대해 1을 제외한 소수점 자리의 값을 나타냄.
exponent: 지수부에 대한 값.
아래의 수식을 보시면 더 직관적으로 이해할 수 있을 것이다.

sign bit는 음수와 양수의 구분을 하고 있다.
fraction은 다소 이해가 되지 않을 수 있는데, 값이 \(1.1011_2\) 이라면, fraction은 1을 제외한 소수점 부분인 1011을 의미한다.
exponent는 bias를 빼줌으로써 계산한다.
실수의 덧셈 연산
이러한 실수의 저장 속에서 실수의 연산을 컴퓨터가 어떻게 하는지에 대해 집중할 필요가 있다.
다시 우리의 목적을 상기해보면 우리는 덧셈을 했을 경우와 곱셈을 했을 경우의 차이에 대해 보고 있었다.
먼저 실수의 덧셈에 대해 확인해 보자.
우리가 생각하고 계산하는 그대로 컴퓨터도 계산한다.
- 먼저 exponent(지수부)를 맞춰준다
- 두 수를 더한다
- scientific-notation으로 다시 정리한다.
- 계산한 후의 값이 1의 자리 숫자에 1이 오도록 연산을 맞춰주는 것을 말한다.
- scientific-notation을 사용해야 1을 제외한 fraction 값을 구할 수 있다.
예시
\(1.01*2^2\) 와 \(1.11*2^0\) 를 더해보자.
- \(1.11*2^0 = 0.0111*2^2\)
- \(2^2\) 의 exponent에 맞추어 지수부를 \(2\) 로 맞춰준다.
- \(1.01*2^2 + 0.0111*2^2 = 1.1011*2^2\)
- 두 수를 더해준다
- \(10.0011 * 2^2 = 1.00011*2^3\)
- scientific-notation을 적용한다
실수의 곱셈 연산
다음은 실수의 곱셈이다.
곰셉은 조금 더 복잡하지만, 간단한 수준의 연산으로 정리된다.
- 먼저 두 수의 exponent를 더해 준다.
- 두 수를 곱한다.
- 그리고 덧셈과 마찬가지로 scientific-notation으로 정리하여 exponent를 다시 계산한다.
예시
\(1.01*2^2\) 와 \(1.11*2^0\) 를 곱해보자.
- \(2 + 0 = 2\)
- 지수부(exponent)를 더해준다.
- \(1.01 * 1.11 = 10.0011\)
- 두 수를 곱해준다.
- \(10.0011 * 2^2 = 1.00011*2^3\)
- scientific-notation을 적용한다
이렇게 덧셈과 곱셈에서의 연산 방식과 차이를 볼 수 있다.
두 연산 방식 모두, double형 기준에서 52bit의 fraction을 초과하는 부분에서 그 이하의 값에 대한 처리가 필요하다는 것을 알 수 있다.
- fraction은 제한적이지만, 실수를 2진수로 저장하면 무제한적이게 길어지기 때문에!
IEEE 754 & JAVA specification
IEEE754에서는 위와 같은 실수의 처리에 대해 여러가지 방법을 제시힌다.
rounding이라고 하는데, 아래와 같은 rounding 방식들을 제시한다.
round to zero, round up, round down, round even, round to nearest
이 중에서도 JAVA는 JAVA specification에서 다음과 같이 round 처리를 밝힌다.

round to nearest: 가까운 곳으로 rounding 하는 방식.
예를 들어서 확실히 이해해보자.
0.1 * 10
0.1과 10의 곱을 나타내면 다음과 같다.
먼저 2진수로 바꿔준 뒤, 이에 대한 52번째 자리까지(fraction이 52bit이기 때문) 계산한 후, 남는 부분을 Round to nearest 처리 해준다.
여기서 nearest는, 값을 버려서 0으로 내림하는 것보다, 1로 올림하는 것이 뒤의 … 값에서 따져봤을 때 더 가까운 값이므로 올려준다.
수식을 정리하면 아래와 같다.
\(0.1\)
\(= 0.00011001100110011001100110011001100110011001100110011001...\)
\(= 0.00011001100110011001100110011001100110011001100110011010\) (Round to nearest)
\(= 1.1001100110011001100110011001100110011001100110011010 *2^{-4}\)
\(10\)
\(= 1010\)
\(= 1.01 * 2^3\)
\(0.1 * 10\)
\(= (1.1001100110011001100110011001100110011001100110011010 *2^{-4}) * (1.01 *2^3)\)
\(= 10.00000000000000000000000000000000000000000000000000001 *2^{-1}\)
\(= 1.0000000000000000000000000000000000000000000000000000\) (Round to nearest)
\(= 1\)
JAVA specification에서 밝히는 규칙을 그대로 따라온 결과, 0.1*10이 1임을 볼 수 있다.
0.1 + 0.1 + …
그렇다면 덧셈의 경우는 어떨까?
보기 좋게 0을 붙여서 scientific-notation form으로 자리수를 맞췄다.
또 헷갈리지 않기 위해 10자리씩 숫자를 나눠 두었다.
| 0.1 + 반복 수 | 저장되는 값 |
|---|---|
| 1 (0.1) | 0.0001 1001100110 0110011001 1001100110 0110011001 1001100110 10 |
| 2 (0.1 + 0.1) | 00.001 1001100110 0110011001 1001100110 0110011001 1001100110 10 |
| 3 | 000.01 0011001100 1100110011 0011001100 1100110011 0011001101 00 |
| 4 | 000.01 1001100110 0110011001 1001100110 0110011001 1001100110 10 |
| 5 | 0000.1 0000000000 0000000000 0000000000 0000000000 0000000000 00 |
| 6 | 0000.1 0011001100 1100110011 0011001100 1100110011 0011001100 11 |
| 7 | 0000.1 0110011001 1001100110 0110011001 1001100110 0110011001 10 |
| 8 | 0000.1 1001100110 0110011001 1001100110 0110011001 1001100110 01 |
| 9 | 0000.1 1100110011 0011001100 1100110011 0011001100 1100110011 00 |
| 10 | 0000.1 1111111111 1111111111 1111111111 1111111111 1111111111 11 |
0.11111111111111111111111111111111111111111111111111111 (2)
= 0.99999999999999988897769753748434595763683319091796875
첫 공백은 각각 fraction 앞의 1을 제외한 수부터 10칸씩을 나타낸다.
따라서 52칸, 52bit의 fraction을 갖는 것을 볼 수 있다.
여기서의 연산에서도, 52bit를 넘어갈 경우 round to nearest를 적용했다.
9번의 연산에 모두 표현하지 못한 점에 대해선 양해가 필요할 것 같다. (힘듦)
- 논리적으로 이해가 되긴 하니까?
주의할 점은 \(0.1 + 0.1\)이 \(0.2\) 가 아니라는 점이다.
\(0.1 != 0.1\) 이기 때문이고, 위에서부터 0.1, 0.1 + 0.1, 0.1 + 0.1 + 0.1을 이어나가 마지막 값이 0.1을 열번 더한 값을 확인할 수 있다. 이 값을 계산기로 계산해보면, 0.9999999... 의 값을 확인할 수 있다.
덧셈의 경우 어렵지 않지만 헷갈릴 수 있다.
한 번의 연산이 일어날 경우, 52bit로 소수점이 잘리며 rounding이 이뤄지는 점에 주목할 필요 가 있다.
위의 연산을 보면,
자리 수가 소수점 넷째 자리에서 첫째 자리까지 바뀌면서,
0.1은 계속해서 넷째 자리이기 때문에,
값의 결과는 계속해서 52bit를 초과하게 되고,
이에 대한 round to nearest가 계속해서 이뤄지게 된다.
코드 및 결과 확인
floating point의 0.1 값을 아래 java 코드로 확인할 수 있다.
@Test
void test() {
double float0_1 = 0.1;
System.out.println(float0_1);
System.out.println(new BigDecimal(float0_1));
byte[] bts = toByteArray(float0_1);
for(int i=0; i<bts.length; i++){
String s1 = String.format("%8s", Integer.toBinaryString(bts[i] & 0xFF)).replace(' ', '0');
System.out.print(s1);
}
}
public static byte[] toByteArray(double value) {
byte[] bts = new byte[8];
ByteBuffer.wrap(bts).putDouble(value);
return bts;
}
0.1 (0.1을 print)
0.1000000000000000055511151231257827021181583404541015625 (0.1을 bigdecimal로 명확하게 print)
0011111110111001100110011001100110011001100110011001100110011010 (0.1의 byte를 출력)
결과
결과적으로 이 글에서는 다음과 같은 내용을 다뤘다.
- 컴퓨터는 소수들에 대해 정확한 표기를 할 수 없다.
- 컴퓨터가 소수를 표기하기 위해 위와 같은 방식을 사용한다.
- IEEE 754에선 소수의 연산을 위한 방식을 표준화하고 있다.
- JAVA는 소수의 연산에 round to nearest를 사용한다.
- 0.1은 0.1이 아니다.
- 0.1 * 10과 0.1 + … + 0.1(10번) 의 값은 다르다.
- 이를 증명하는 방법들.
이와 관련해서 C나 다른 언어에서는 다른 값을 보일 수 있다는 것도 참고해야 한다.
언어마다 IEEE 754에서 보이는 round 규칙 중 다른 것을 택하기 때문이다.